By Amanda Morrall

Albert Einstein described compound interest as the Eighth Wonder of the World. He said “those who understand compound interest earn it, and those who don’t, pay it”. Looking at the high level of credit card debt that exists in New Zealand and worldwide, many people are in the latter category of Einstein's statement. According to a McKinsey survey, roughly 60% of credit card holders don’t pay the full amount on their monthly statements. And when you consider the average credit card balance for Kiwis is $5,973 and the standard credit card rate is 19.8%, ignorance can be a high price to pay.

Compound interest is how some people get into trouble and how others benefit financially - ever heard of the saying “the rich get richer and the poor get poorer”? Sure, some people may understand the cost of borrowing - but can’t afford to reduce their debt. Curiously though, many people will sit on savings while their debt mountain grows, or make spending decisions that can exacerbate their problem.

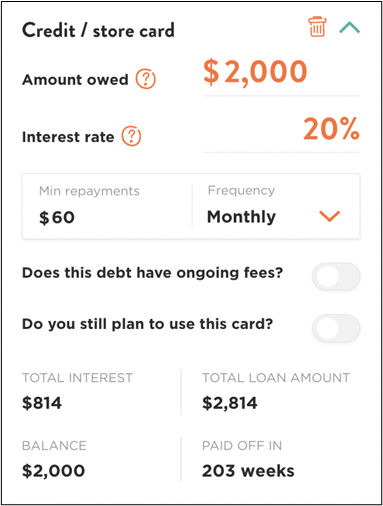
Simply put, compound interest is the interest you pay on a loan or receive on a deposit, which gets calculated on the initial principal plus the previously accumulated interest - meaning it increases exponentially - rather than linearly - over time. The key word here is ‘compound’. Take this example using Sorted.org’s debt calculator tool (which you can find here):

Jane buys a $2,000 computer on her credit card at 20% interest. Each month she pays $60 (around 3% of the principal), which is roughly the minimum amount. At that level of repayment, it takes Jane 203 weeks to pay off her computer, and she’s added an extra $814 to the total cost because of compounding interest. So that $2,000 computer really cost Jane $2,814 when you factor in the compounded interest she had to pay.

Here’s an example where compound interest can work in your favour:

Bob invests $1,000 at an annualised interest rate of 5%. After the first year, Bob earns $50 in interest ($1000 x 0.05 = $50). In the second year, instead of earning interest on just the original $1,000, Bob earns interest on the new total of $1050 (original principal of $1000 plus $50 in interest). So, in the second year, Bob earns $52.50 in interest ($1050 x 0.05 = $52.50), and his original $1,000 grows to $1,102.50. If Bob left his $1,000 and invested no more, after 15 years at the same 5% interest rate, he would end up with $2,078.93. The total interest earned for that period would be $1,078.93.

The frequency of compounding can make a significant difference in the interest earned or paid over time. If Bob were earning interest compounded monthly (rather than yearly) on that $1,000 over 15 years, he could end up with $2,113.70 - the interest portion being $1,113.70.

The good thing is, you don’t have to be a math expert to figure this out. There are many free interest calculation tools available online; you just need to plug in your numbers. The Government’s financial education website Sorted is a great resource, as is MoneyHub - which provides guides and calculators on a range of topics.

So how does compounding interest work with investment management fees? As you’ll see in the following example, it has the effect of eating into your savings over time.

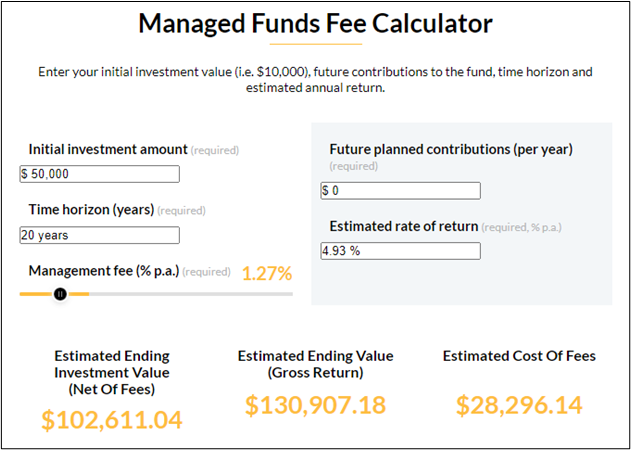
Let’s take an example using MoneyHub’s Managed Funds calculator. On a one-time lump sum investment of $50,000, earning a rate of return of 4.93%^ p.a. over 20 years and paying the average management fee of 1.27%*, the expected after-fee return using the calculator would be $102,611.04. The fees paid on that would be around $28,296.14:

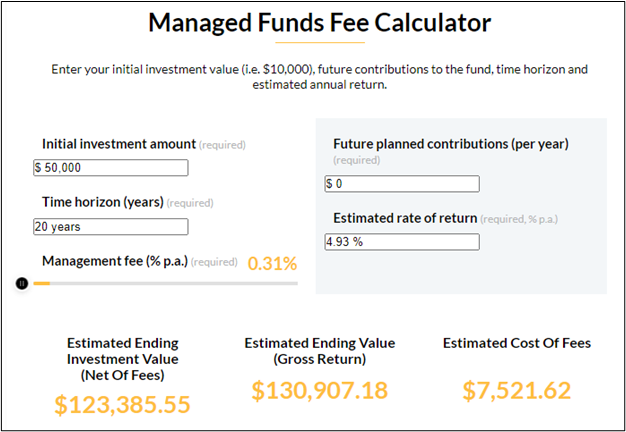
In the same scenario using MoneyHub’s Managed Fund calculator but plugging in a management fee of 0.31%, the after-fee return would be $123,386. The fees would be $7,521, a total difference of almost $20,775 over 20 years:

To find out what you are paying annually in fees with various providers, check out our fee comparison tool here. It will show you a snapshot in time only, not the compound effect of fees, but it will give you some idea of how big the difference is even over just one year, and what the implications are over time.

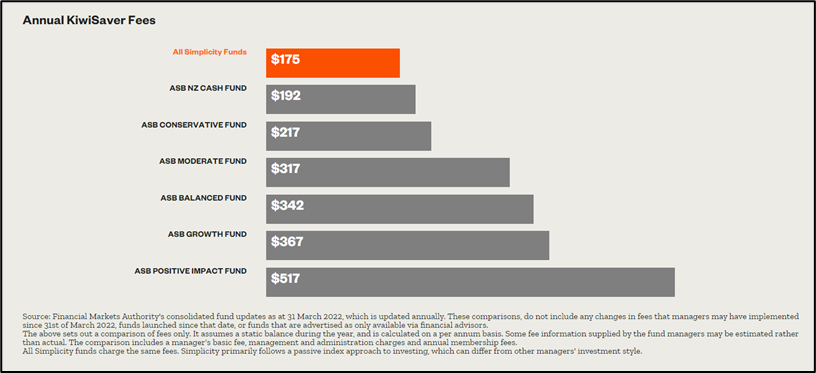
Below is an example of the KiwiSaver annual fee differences comparing Simplicity to ASB, which, similar to Simplicity, has a passive index tracking approach to investing for most asset classes, on a balance of $50,000. You can see the annual fees vary depending on fund type for ASB, whereas Simplicity charges the same annual fee regardless of fund type in its KiwiSaver Scheme:

Fees are one component affecting your investment over time. Investment returns or losses, contribution rates and tax will also significantly impact your savings outcomes (see our blog on doing a KiwiSaver health check for more info on these). But unlike investment returns, which are volatile and extremely hard to predict, you can decide how much you pay in fees. It all starts with an understanding of how much you’re being charged.

Depending on whether you’re a borrower or investor, by understanding it well, you’ll either love or hate compounding interest.


Notes:

^As at the date of this post, according to sorted.org.nz the average annual return for KiwiSaver growth funds (after fees and taxes, measured over the last 5 years) is 4.93%.

*As at the date of this post, according to sorted.org.nz the average total annual fee for a KiwiSaver growth fund for the past year (based on a $10,000 balance, and including both flat fees for membership and percentage fees) is 1.27%.

The information provided and opinions expressed in this post are intended for general guidance only and not personalised to you. These materials do not take into account your particular financial situation or goals and are not financial advice or a recommendation. This post is not intended to convey any guarantees as to the future performance of any of the investment products, asset classes, or capital markets mentioned. Past performance is no guarantee of future performance. Information is current at the time of posting, and subject to change without notice.